| |||||||||||||||||||||||
 | |||||||||||||||||||||||
| 動機 | |||||||||||||||||||||||
|
まず,なぜ「待ち行列」なるものを考えないといけないのか,そもそもどうしてそんな理論が必要なのか,という動機を理解することからはじめます. 風邪をひいちゃった.
病院に行きたいんだけど混んでるしなぁ, 病院行ってかえってこじらしたらやだな. *** どのくらい待つんだろう? *** こんな素朴な疑問,誰でももちますよね.この待ち時間を定量的に求めたい,という のが動機です.もちろん確率の問題ですから,正確には *** 平均どのくらい待つか ***
というのがいいでしょう.これに答えを出すのが「待ち行列理論」ということになります. | |||||||||||||||||||||||
| 必要な情報 | |||||||||||||||||||||||
|
さて,前もって何も情報がなくて「どのくらい待つんだろう」という問には答えられませんね.これの答えを出すためには, *** どのくらい混んでいるの? ***
という情報が必要です.混み具合も確率の問題となるため, *** 平均どのくらい混んでいるか ***
というのがより正確です.驚くべきとこに,「どのくらい混んでいるか」さえ 分かれば,「どのくらい待つか」という答えがでるのです.これが,この理論の強力なところです. すこし形式的な言い方をすれば,待ち行列理論では,「平均待ち時間」は, 「混み具合」という変数のみの関数として表現されます. | |||||||||||||||||||||||
| いきなり結論 | |||||||||||||||||||||||
|
さて,一気に結論を言ってしまいます.「混み具合」を「ρ」(ロー)というギリシャ文字で表すと,あなたが医者に行くと,あなたの待つ時間は,
待ち時間 = ρ/(1-ρ) [人分]
です.なんとシンプルなんでしょうか!(驚いて下さい) ここで,[人分]と書いたのは,あなたの前にはすでにρ/(1-ρ)人が並んで待っているということです.実は,この式にはいろんな前提が含まれているのですが,それは置いておいて,待ち行列理論の肝はこの式です.これさえ理解していれば大丈夫.なお,待ち時間の単位については,後で説明します. 0 <= ρ <= 1 でこの式のグラフを書いてみましょう. 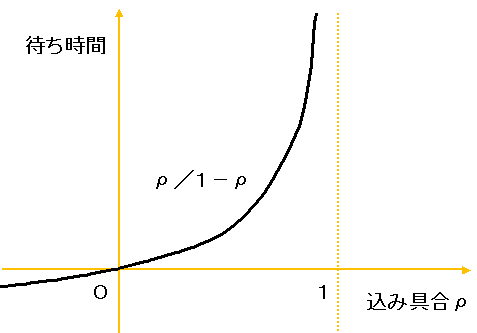 ρ/(1-ρ) = -1/(ρ-1) -1
ですから,y=1/x の双曲線をy軸対称に反転し,(1,-1) だけ平行移動したものです. ρ=0 の時に待ち時間は 0 です.ρ=1 に近付くにつれて,待ち時間は急激にはね上がります.ρ=1 では∞になります.(永久に待たされます) | |||||||||||||||||||||||
| 混み具合の表現 | |||||||||||||||||||||||
|
さて,では「どのくらい混んでいるか」というのをもう少し正確に定義してみます. 先の病院の例を使うことにします. 混み具合は,「患者がどの位頻繁にくるのか」と「お医者さんがどの位手際良く患者 を診るか」という2つの独立した要素に左右されます. 「λ」(ラムダ)というギリシャ文字を使って,患者がどのくらい頻繁にくるかを表します.つ まり,「1時間に何人患者がくるか」という量です.これを,「平均到着率」といい ます.この「λ」という文字を良く見ると,頭をうなだれてとぼとぼ歩く患者のイメージが湧きます. λ ..... とぼとぼ歩く患者...とぼとぼとぼ
次に,「μ」(ミュー)というギリシャ文字を使って,お医者さんの診察の手際良さを表します. つまり,「1時間に何人の患者を診察するか」という量です.これを「平均サービス 率」といいます(自分をサービス業だと思っている医者が増えるとよいですね).この 「μ」という文字を良く見ると,お医者さんのカルテのサインに見えませんか?お医者さ んはドイツ語(最近は英語でしょうか)でカルテを書きます.さらさらと書くので,何 が書いてあるのか気にはなりますがよくわかりません.そのカルテの末尾のサインを この文字からイメージしてください. μ ..... さらさら書く医者のカルテ...さらさらさら
混み具合は,患者が訪れる頻度と,医者の手際に掛かっています.次のようなモデルを考えると分かりやすいでしょう.
ここで,混み具合「ρ」を表す準備ができました.λとμの比率がρです. ρ = λ/μ (混み具合) ... 利用の回転... くるくる
2つの量の比率をとっています.この量でもって,病院の「混み具合」を表現しま す.ρという字から,サービスがくるくる回る感じをイメージします. この量を「平均利用率」と言います.この量が大きければ「混んでいる」,小さ ければ「すいている」ということです.平均利用率「平均トラフィック密度」, という言葉も使用されます. ρには単位がありません.単なる比率ですから,0 から 1 までの値,あるいは, 0% から 100% までの値をとります.これに対して,λとμは時間を分母に持ちます. 時間の単位はλとμで同じであればなんでもよいです. もう少し補足します.λは1時間に何人来るか,という量ですが,この逆数を,Ta と いう記号を使って「平均到着時間」と言います.つまり,何時間おきに患者は来る か,という量です(a は arrival の a です). また,μは1時間に何人診るか,という量ですが,この逆数を, Ts という記号を 使って「平均サービス時間」と言います.つまり,1人あたり何時間掛かるか,とい う量です(s は service の s です).
これで,どれくらい混んでいるか,が定式化できました. | |||||||||||||||||||||||
| 待ち時間 | |||||||||||||||||||||||
|
最初に書いたように,「どれくらい混んでいるか」から「どれくらい待つか」を求め るのが待ち行列理論でしたよね.混み方が定式化できたのだから,もう答えを出してもよいでしょう. 理論の詳細は省き,結論だけ覚えてしまいましょう.答えは, ρ/(1-ρ) 人分待つ
です.一人当たりTsの時間が掛かるとすると,待つ時間を Tw (w は wait) は, Tw = (ρ/(1-ρ)) Ts
とも言えます.あなたが医者へ着いたときには,すでにρ/(1-ρ)人待っているでしょう.と言ってもいいです. これで理論はすべてです. |
| 練習 | |||
|
では,実際の情報処理試験の問題を一問解いて見ましょう. ある医院では,患者が平均10分間隔でランダムに訪ねてくる。医者は、1人であり、一人の患者の診断および処方の時間は平均8分の指数分布であった。このとき,患者が診察を受け始めるまでの純粋待ち時間は何分か。 上記の問題には,「ランダムに」とか「指数分布」とか書かれています. 実は,これまでの理論はすべて,到着がランダムであること(ポアソン分布), それから平均サービス時間が指数分布であることが前提でしたが, わかりやすさのために,説明を省いていました.ここでは,この条件が, そろっているのでこれまでの理論をそのまま使うことができます. さて,順に考えます.まずλ(とぼとぼ)とμ(さらさら)を求め,そこから混み具合ρを求めましょう. λ(とぼとぼ)は,Ta(平均到着時間)の逆数ですから, λ = 1/10 [人/分]
です.すなわち,1分に 0.1 人到着します.少数が出てくると分かりにくい人は, λ = 6 [人/時間]
と考え,1時間で6人くる,と考えて下さい. μ(さらさら)は,Ts(平均サービス時間)の逆数ですから, μ = 1/8 [人/分]
です.すなわち,1分に 0.125 人診察します.また,時間で考えると, μ = 7.5 [人/時間]
です.
という状況ですね. よって,ρ(混み具合)は,どちらの単位でも同じで, ρ = (1/10)/(1/8) = 6/7.5= 0.8
となります.つまり混雑度は 80% ということです.すると,待ちは, ρ/(1-ρ) = 0.8/(1-0.8) = 4 [人分]
です.1人あたりの診察時間が Ts = 8分なので,待ち時間は, 4 * 8 [分] = 32 [分]
ということになります.問題文中,「純粋待ち時間」というのは 「自分が診てもらっている時間を含めない」ということです.自分 の診察まで含めて,医者での診察が終了するまでの時間は, 32 + 8 = 40 分
となります.自分のサービス時間も含める場合が重要になることが あります.その時間は「ターンアラウンド」タイムと言います. ネットワークなどの待ち時間の問題では,「ターンアラウンド」時 間,すなわち,キーを押してからその反応が戻って来るまでの時間が求められることが多いからです. | |||
| 窓口が倍,列も倍になった場合 | |||
|
この問題で,窓口の数が倍になった場合,すなわち、サービス時間はそのままで患者が平均的に2つの列に分かれて待つようにするとします。例えば病院を2つ建てた場合などです。そうすると、混み具合も半分になります。 μは変わりませんが,λが 6 から 3 になり,ρは半分の 0.4 となりますね.
μ=7.5[人/時間]
λ=3[人/時間] ρ=3/7.5=0.4 待ち=0.4/(1-0.4)=0.67[人分] 待ち時間=0.67*8[分]=5.3[分] ターンアラウンドタイム=5.3+8=13.3[分] 待ち時間が32[分]から5.3[分]と80%以上改善されます.約6倍です.ターンアラウンドタイムも約67%改善されます. ちなみに,窓口が2つで,列が1つの場合は、M/M/2モデルになりますので,また違う式になります. |
| サービス時間が半分になった場合 |
|
今度は,お医者の能力が上がって,サービス時間が半分になった場合を考えて見ます.
μ=15[人/時間]
ρ=6/15=0.4 待ち=0.4/(1-0.4)=0.67[人分] とここまでは、窓口が倍と同じです.しかし,サービス時間が半分になっているので、同じ待ち人数でも待ち時間は半分です。 待ち時間=0.67*4[分]=2.7[分] この場合待ち時間は,32[分]から2.7[分]と90%以上改善されます.約12倍にもなります.ターンアラウンドタイムも約83%改善されます. 倍の人数を雇うよりも、2倍の能力を持った人を2倍の給料で雇うほうがお得って感じでしょうか. |
| おわりに |
|
とっても大雑把に,待ち行列の理論を解説してみました.ここでの お話は,M/M/1と分類される待ち行列です.サービス時間 の分布や到着時間の分布,窓口の数などでこの式は変わりますが, ここまで理解できれば,分かったような気になるには十分だと思います. では,次に医者に行くときは,とぼとぼと頭をうなだれて行かないように 気をつけましょう. おしまい |
| おまけ 窓口が倍で1列の場合 |
|
ちょっとだけややこしいM/M/2モデルのお話になります.ややこしいといっても,回転率を2乗にするだけです. Tw=(ρ^2/(1-ρ^2))Ts
窓口が2倍になって処理能力が倍になるので,回転率ρは
μ=7.5*2=15[人/時間]
ρ=6/15=0.4 この式で待を求めると,窓口が2倍になって処理能力が倍になるので,待ちは (ρ^2/(1-ρ^2))Ts=(0.4^2/(1-0.4^2))
=0.16/(1-0.16)=0.19[人分] サービス時間は8[分]ですから 待ち時間=0.19[人分]*8[分]=1.5[分]
ターンアラウンドタイム=1.5+8=9.5[分] なんと,待ち時間は32[分]から1.5[分]と95%以上の改善です.ターンアラウンドタイムについては約76%となり,サービス時間を半分に短縮したほどではありませんが,なかなかの効果ですね. |
| 謝辞 |
|
この記事に関して,高戸秀明さん,天野勝さん,高嶋優子さん,斎藤末広さん,益田秀樹さん,倉谷和彦さん,山田雄介さんより有用なコメントを頂きました.どうもありがとうございました.
Kenji Hiranabe <hiranabe@esm.co.jp> Last modified: Thu May 1 13:22:08 2008 |

